1. Verificació del principi físic de la fórmula bàsica
Llei de conservació de la massa
Totes les fórmules es basen en la naturalesa física de m=ρ×V (massa = densitat × volum)
Valor de densitat
Densitat teòrica de l'alumini pur: 2.698 kg/m³ (20 ℃)
El valor aproximat de 2.700 kg/m³ és raonable per a càlculs industrials (error < 0,1%)
2. Verificació del rigor de les fórmules geomètriques
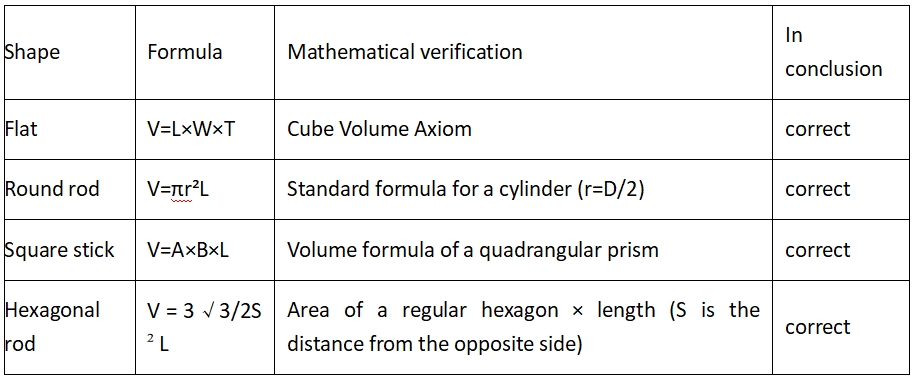
2.1. Fórmula estàndard del volum geomètric
Restriccions de la fórmula del tub quadrat:
Això és cert quan el gruix de la paret del tub és uniforme i l'angle interior és un angle recte (el tub quadrat real té una transició arrodonida i l'error teòric és d'aproximadament 1-3%).
3. Verificació de la coherència del sistema d'unitats
Investigació de punts de risc de càlcul entre unitats
4. Esmena d'idoneïtat d'enginyeria
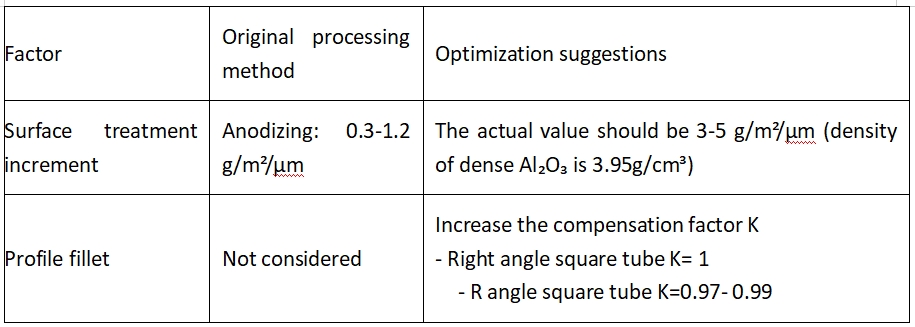
4.1. Compensació per factors no ideals
4.2. Quantificació de l'impacte de la tolerància
Tolerància de gruix ±10% → Desviació de pes ±(8% ~ 12%) (les peces de paret fina són més sensibles)
Solució: W real = W teòric × (1 + Δt / t) (Δt: desviació del gruix)
5. Prova de condicions de contorn
Verificació de casos extrems:
Escenari d'anomalia de densitat
Aliatge 7xxx (7075): Densitat mesurada 2,810 g/cm³ → Si s'utilitza 2,7 g/cm³ per error, l'error és del +4,1%.
Taula de fórmules
4t(A + B) - 4t² és un càlcul d'enginyeria estàndard que es calcula multiplicant el perímetre de la secció pel gruix de la paret i després restant les quatre cantonades.
Exemple de càlcul:
Placa d'alumini 1.6061(1000 × 500 × 10 mm, longitud 2 m): A = 1000 × 500 × 2 × 0,0027 = 27 kg
Tub rodó 2.7075(diàmetre exterior 50 mm, gruix de paret 3 mm, longitud 1,5 m): W = [(50-3)×3×3,1416×1,5]×0,00283 ≈ 5,65 kg
3. Tub quadrat(40 × 40 × 2 mm, longitud 3 m): W = [2 × 2 × (40 + 40 - 4) × 3] × 0,0027 × 0,98 ≈ 2,42 kg
Flux de treball recomanat
1. Seleccioneu la densitat → 2. Mesureu la mida real → 3. Seleccioneu el factor de compensació → 4. Calculeu mitjançant la fórmula
Data de publicació: 17 de juny de 2025