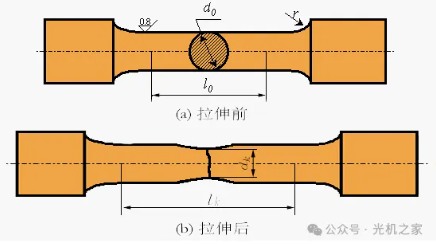
La prova de resistència a la tracció s'utilitza principalment per determinar la capacitat dels materials metàl·lics per resistir danys durant el procés d'estirament, i és un dels indicadors importants per avaluar les propietats mecàniques dels materials.
1. Prova de tracció
La prova de tracció es basa en els principis bàsics de la mecànica de materials. En aplicar una càrrega de tracció a la mostra de material sota certes condicions, es provoca una deformació per tracció fins que la mostra es trenca. Durant la prova, es registra la deformació de la mostra experimental sota diferents càrregues i la càrrega màxima quan la mostra es trenca, per tal de calcular el límit elàstic, la resistència a la tracció i altres indicadors de rendiment del material.
Tensió σ = F/A
σ és la resistència a la tracció (MPa)
F és la càrrega de tracció (N)
A és l'àrea de la secció transversal de la mostra
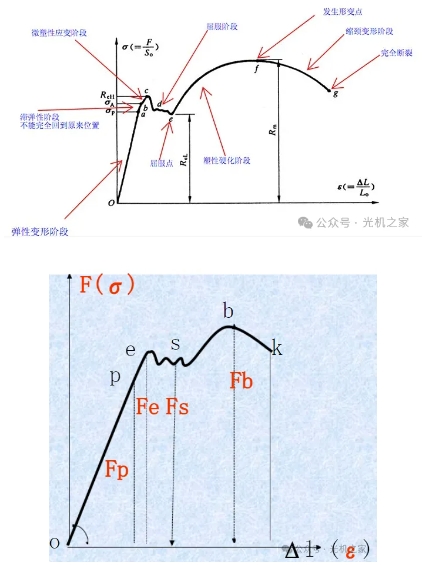
2. Corba de tracció
Anàlisi de diverses etapes del procés d'estirament:
a. A la fase OP amb una càrrega petita, l'elongació està en una relació lineal amb la càrrega, i Fp és la càrrega màxima per mantenir la línia recta.
b. Després que la càrrega superi Fp, la corba de tracció comença a adoptar una relació no lineal. La mostra entra a la fase de deformació inicial, es retira la càrrega i la mostra pot tornar al seu estat original i deformar-se elàsticament.
c. Després que la càrrega superi Fe, la càrrega s'elimina, es restaura part de la deformació i es reté part de la deformació residual, cosa que s'anomena deformació plàstica. Fe s'anomena límit elàstic.
d. Quan la càrrega augmenta encara més, la corba de tracció mostra una forma de dent de serra. Quan la càrrega no augmenta ni disminueix, el fenomen d'elongació contínua de la mostra experimental s'anomena cediment. Després de la cediment, la mostra comença a patir una deformació plàstica evident.
e. Després de la tracció, la mostra mostra un augment de la resistència a la deformació, l'enduriment per deformació i l'enfortiment per deformació. Quan la càrrega arriba a Fb, la mateixa part de la mostra es contrau bruscament. Fb és el límit de resistència.
f. El fenomen de la contracció provoca una disminució de la capacitat portant de la mostra. Quan la càrrega arriba a Fk, la mostra es trenca. Això s'anomena càrrega de fractura.
Força de rendiment
El límit elàstic és el valor màxim de tensió que un material metàl·lic pot suportar des del començament de la deformació plàstica fins a la fractura completa quan se sotmet a una força externa. Aquest valor marca el punt crític on el material passa de l'etapa de deformació elàstica a l'etapa de deformació plàstica.
Classificació
Límit elàstic superior: es refereix a la tensió màxima de la mostra abans que la força disminueixi per primera vegada quan es produeix el lligament.
Límit elàstic inferior: es refereix a la tensió mínima en l'etapa elàstica quan s'ignora l'efecte transitori inicial. Com que el valor del punt elàstic inferior és relativament estable, normalment s'utilitza com a indicador de la resistència del material, anomenat punt elàstic o límit elàstic.
Fórmula de càlcul
Per al límit elàstic superior: R = F / Sₒ, on F és la força màxima abans que la força disminueixi per primera vegada a l'etapa de límit elàstic, i Sₒ és l'àrea de la secció transversal original de la mostra.
Per a un límit elàstic més baix: R = F / Sₒ, on F és la força mínima F ignorant l'efecte transitori inicial, i Sₒ és l'àrea de la secció transversal original de la mostra.
Unitat
La unitat de límit elàstic sol ser MPa (megapascal) o N/mm² (Newton per mil·límetre quadrat).
Exemple
Prenguem com a exemple l'acer baix en carboni, el seu límit de rendiment sol ser de 207 MPa. Quan se sotmet a una força externa superior a aquest límit, l'acer baix en carboni produirà una deformació permanent i no es podrà restaurar; quan se sotmet a una força externa inferior a aquest límit, l'acer baix en carboni pot tornar al seu estat original.
El límit elàstic és un dels indicadors importants per avaluar les propietats mecàniques dels materials metàl·lics. Reflecteix la capacitat dels materials per resistir la deformació plàstica quan se sotmeten a forces externes.
Resistència a la tracció
La resistència a la tracció és la capacitat d'un material per resistir danys sota càrrega de tracció, que s'expressa específicament com el valor màxim de tensió que el material pot suportar durant el procés de tracció. Quan la tensió de tracció del material supera la seva resistència a la tracció, el material experimentarà deformació plàstica o fractura.
Fórmula de càlcul
La fórmula de càlcul de la resistència a la tracció (σt) és:
σt = F / A
On F és la força de tracció màxima (Newton, N) que la mostra pot suportar abans de trencar-se, i A és l'àrea de la secció transversal original de la mostra (mil·límetre quadrat, mm²).
Unitat
La unitat de resistència a la tracció sol ser MPa (megapascal) o N/mm² (Newton per mil·límetre quadrat). 1 MPa és igual a 1.000.000 de Newtons per metre quadrat, que també és igual a 1 N/mm².
Factors d'influència
La resistència a la tracció es veu afectada per molts factors, com ara la composició química, la microestructura, el procés de tractament tèrmic, el mètode de processament, etc. Diferents materials tenen diferents resistències a la tracció, per la qual cosa en aplicacions pràctiques cal seleccionar materials adequats en funció de les propietats mecàniques dels materials.
Aplicació pràctica
La resistència a la tracció és un paràmetre molt important en el camp de la ciència i l'enginyeria de materials, i sovint s'utilitza per avaluar les propietats mecàniques dels materials. Pel que fa al disseny estructural, la selecció de materials, l'avaluació de la seguretat, etc., la resistència a la tracció és un factor que s'ha de tenir en compte. Per exemple, en l'enginyeria de la construcció, la resistència a la tracció de l'acer és un factor important per determinar si pot suportar càrregues; en el camp de l'aeroespacial, la resistència a la tracció dels materials lleugers i d'alta resistència és la clau per garantir la seguretat de les aeronaus.
Resistència a la fatiga:
La fatiga metàl·lica es refereix al procés en què els materials i components produeixen gradualment danys acumulatius permanents locals en un o diversos llocs sota estrès cíclic o deformació cíclica, i es produeixen esquerdes o fractures completes sobtades després d'un cert nombre de cicles.
Característiques
Sobteïtat en el temps: La falla per fatiga metàl·lica sovint es produeix de sobte en un curt període de temps sense signes evidents.
Localitat en posició: La falla per fatiga sol produir-se en zones locals on es concentra l'estrès.
Sensibilitat a l'entorn i als defectes: la fatiga metàl·lica és molt sensible a l'entorn i als petits defectes de l'interior del material, que poden accelerar el procés de fatiga.
Factors d'influència
Amplitud de la tensió: La magnitud de la tensió afecta directament la vida a fatiga del metall.
Magnitud de la tensió mitjana: Com més gran sigui la tensió mitjana, més curta serà la vida a fatiga del metall.
Nombre de cicles: Com més vegades el metall estigui sota tensió o deformació cíclica, més greu serà l'acumulació de danys per fatiga.
Mesures preventives
Optimitzar la selecció de materials: seleccionar materials amb límits de fatiga més alts.
Reducció de la concentració d'estrès: Reduir la concentració d'estrès mitjançant el disseny estructural o mètodes de processament, com ara l'ús de transicions de cantonades arrodonides, l'augment de les dimensions de la secció transversal, etc.
Tractament superficial: polit, polvorització, etc. sobre la superfície metàl·lica per reduir els defectes superficials i millorar la resistència a la fatiga.
Inspecció i manteniment: Inspeccioneu regularment els components metàl·lics per detectar i reparar ràpidament defectes com ara esquerdes; feu el manteniment de les peces propenses a la fatiga, com ara substituir les peces desgastades i reforçar els enllaços febles.
La fatiga metàl·lica és un mode de fallada metàl·lica comú, que es caracteritza per la sobtadesa, la localitat i la sensibilitat a l'entorn. L'amplitud de la tensió, la magnitud mitjana de la tensió i el nombre de cicles són els principals factors que afecten la fatiga metàl·lica.
Corba SN: descriu la vida a fatiga dels materials sota diferents nivells d'estrès, on S representa l'estrès i N representa el nombre de cicles d'estrès.
Fórmula del coeficient de resistència a la fatiga:
(Kf = Ka ∫Kb ∫Kc ∫Kd ∫Ke)
On (Ka) és el factor de càrrega, (Kb) és el factor de mida, (Kc) és el factor de temperatura, (Kd) és el factor de qualitat superficial i (Ke) és el factor de fiabilitat.
Expressió matemàtica de la corba SN:
(\sigma^m N = C)
On (σ) és la tensió, N és el nombre de cicles de tensió i m i C són constants del material.
Passos de càlcul
Determineu les constants materials:
Determineu els valors de m i C mitjançant experiments o consultant la literatura pertinent.
Determineu el factor de concentració d'estrès: considereu la forma i la mida reals de la peça, així com la concentració d'estrès causada pels filetes, les ranures, etc., per determinar el factor de concentració d'estrès K. Calculeu la resistència a la fatiga: segons la corba SN i el factor de concentració d'estrès, combinats amb la vida útil de disseny i el nivell d'estrès de treball de la peça, calculeu la resistència a la fatiga.
2. Plasticitat:
La plasticitat fa referència a la propietat d'un material que, quan se sotmet a una força externa, produeix una deformació permanent sense trencar-se quan la força externa supera el seu límit elàstic. Aquesta deformació és irreversible i el material no tornarà a la seva forma original encara que es retiri la força externa.
Índex de plasticitat i la seva fórmula de càlcul
Elongació (δ)
Definició: L'allargament és el percentatge de la deformació total de la secció de calibre després que la mostra es fracturi per tracció fins a la longitud de calibre original.
Fórmula: δ = (L1 – L0) / L0 × 100%
On L0 és la longitud de calibre original de la mostra;
L1 és la longitud de calibre després de trencar la mostra.
Reducció segmentària (Ψ)
Definició: La reducció segmentària és el percentatge de la reducció màxima de l'àrea de la secció transversal en el punt de coll després que la mostra es trenqui fins a l'àrea de la secció transversal original.
Fórmula: Ψ = (F0 – F1) / F0 × 100%
On F0 és l'àrea de la secció transversal original de la mostra;
F1 és l'àrea de la secció transversal en el punt de coll després que la mostra es trenqui.
3. Duresa
La duresa dels metalls és un índex de propietats mecàniques que mesura la duresa dels materials metàl·lics. Indica la capacitat de resistir la deformació en el volum local de la superfície metàl·lica.
Classificació i representació de la duresa dels metalls
La duresa dels metalls té diversos mètodes de classificació i representació segons els diferents mètodes d'assaig. Principalment s'inclouen els següents:
Duresa Brinell (HB):
Àmbit d'aplicació: Generalment s'utilitza quan el material és més tou, com ara metalls no ferrosos, acer abans del tractament tèrmic o després del recuit.
Principi de prova: Amb una determinada mida de càrrega de prova, una bola d'acer endurit o una bola de carbur d'un cert diàmetre es prem a la superfície del metall a provar, i la càrrega es descarrega després d'un temps especificat, i es mesura el diàmetre de la indentació a la superfície a provar.
Fórmula de càlcul: El valor de la duresa Brinell és el quocient que s'obté dividint la càrrega per la superfície esfèrica de la indentació.
Duresa Rockwell (HR):
Àmbit d'aplicació: Generalment s'utilitza per a materials amb una duresa més alta, com ara la duresa després del tractament tèrmic.
Principi de prova: Similar a la duresa Brinell, però utilitzant diferents sondes (diamant) i diferents mètodes de càlcul.
Tipus: Segons l'aplicació, hi ha HRC (per a materials d'alta duresa), HRA, HRB i altres tipus.
Duresa Vickers (HV):
Àmbit d'aplicació: Apte per a anàlisis amb microscopi.
Principi de prova: premeu la superfície del material amb una càrrega inferior a 120 kg i un indentador de con quadrat de diamant amb un angle de vèrtex de 136° i dividiu la superfície del forat d'indentació del material pel valor de la càrrega per obtenir el valor de duresa Vickers.
Duresa Leeb (HL):
Característiques: Duròmetre portàtil, fàcil de mesurar.
Principi de prova: utilitzeu el rebot generat pel capçal de la bola d'impacte després d'impactar la superfície de duresa i calculeu la duresa mitjançant la relació entre la velocitat de rebot del punxó a 1 mm de la superfície de la mostra i la velocitat d'impacte.
Data de publicació: 25 de setembre de 2024